Math Unit 6 Homework Answers. Interserve Industrial Unit 2, Olympic Park, Poole Hall Road Nusteel Structures Solent Protective Coatings Ltd Ellesmere Port, Cheshire, CH66 1ST Lympne Industrial Estate, Lympne, Hythe, Tredegar Wharf, Marine Parade T: 01 Kent, CT21 4LR Southampton, Hants, SO14 5JF T: 12 T: 80.
- Old Unit 2 Agendamrs. Colville's Math Class 6
- Old Unit 2 Agendamrs. Colville's Math Classroom
- Old Unit 2 Agendamrs. Colville's Math Classes
1.1
Estimation & Mental Math. Use mental math strategies to add and subtract. Identify $1, $5, $10, and $20 bills. Count and make combinations of coins and bills. Compare money amounts. Use the dollar sign and decimal point. Solve addition and subtraction money problems. Fraction Concepts, Operations & Applications. This class primarily uses the Project M2: Mentoring Mathematical Minds curriculum, which is geared toward students showing high ability in mathematics and units from the Center of Gifted Education at the College of William & Mary. These lessons motivate and challenge students, while focusing on critical and creative problem-solving and reasoning. We would like to show you a description here but the site won’t allow us.

1.
Soln:
A man can enter the stadium in 4 ways. Again the man can leave the stadium in 9 ways.
So, total no.of ways with which a man enters and then leaves the stadium = 4 * 9 = 36ways.
2.
Soln:
There are 6 choices for a student to enter the hostel. There are 5 choices for a student to leave the hostel as different door is to be used.
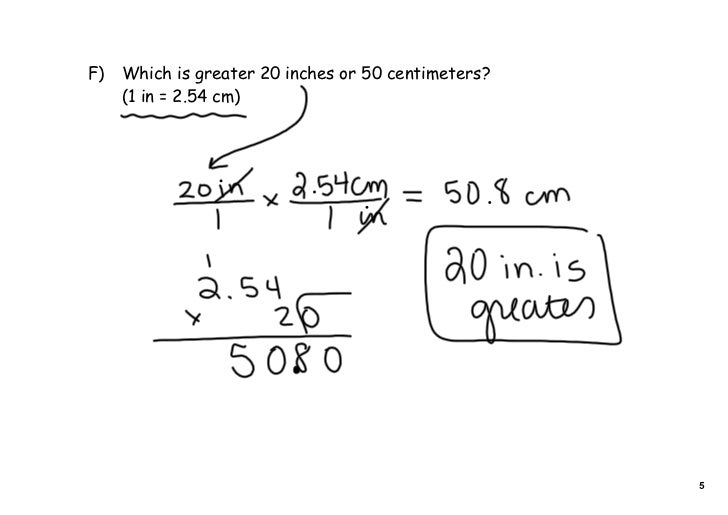
So, total no.of ways = 6 * 5 = 30.
3.
Soln:
There are 7 choices for 1st son, 6 choices for 2nd son and 5 choices for 3rd son.
Now, by the basic principle of counting, the total number of ways of choice = 7 * 6 * 5 = 210.
4.
Soln:
A man can go from city A to city B in 5 ways. As he has to return by a different road, so he can return from city B to city A in 4 ways.
Old Unit 2 Agendamrs. Colville's Math Class 6
So, total no.of ways by which a man can go from city A to city B and returns by a different road = 5 * 4 = 20 ways.

5.
Soln:
A person can go from city A to city B in 5 ways. Again, he can go from city B to city C in 4 ways. So, a person can go from city A to city C in 5 * 4 = 20ways. The person has to return from C to A without driving on the same road twice, So, he can return from city C to city B in 3 ways and from city B to city A in 4 ways.
So, he can return from city C to city A in 3 * 4 = 12 ways.
So, Total no.of ways by which a person can go from city A to city C and return from city C to city A = 20 * 12 = 240 ways.
6.
Soln:
Numbers formed should be of at least 3 digits means they may be of 3 digits, 4 digits, 5 digits or 6 digits.
There are 6 choices for digit in the units place. There are 5 and 4 choices for digits in ten and hundred’s place respectively.
So, total number of ways by which 3 digits numbers can be formed = 6.5.4 = 120
Similarly, the total no.of ways by which 4 digits numbers can be formed = 6.5.4.3 = 360.
the total no. of ways by which 5 digits numbers can be formed = 6.5.4.3.2 = 720.
The total no.of ways by which 4 digits numbers can be formed = 6.5.4.3.2.1 = 720.
So, total no.of ways by which the numbers of at least 3 digits can be formed = 120 + 360 + 720 + 720 = 1920.
7.
Soln:
The numbers formed must be of three digits and less than 500, so the digit in the hundred’s place should be 1,2,3 or 4. So, there are 4 choices for the digit in the hundred’s place. There are 5 choice for the digit in the ten’s place. There are 4 choices for the digit in the unit’s place.
So, no of ways by which 3 digits numbers les than 500 can be formed = 4.5.4 = 80.
8.
Soln:
The numbers formed should be even. So, the digit in the unit’s place must be 2 or 4. So, the digit in unit’s place must be 2 or 4. So, for the digit in unit’s place, there are 2 choices. So, after fixing the digit in the unit’s place, remaining 4 figures can be arranged in P(4,4) ways.
Ie. $frac{{left( 4 right)!}}{{left( {4 - 4} right)!}}$ = $frac{{4!}}{{0!}}$ = $frac{{4{rm{*}}3{rm{*}}2{rm{*}}1}}{1}$ = 24 ways.
So, total no.of ways by which 5 even numbers can be formed = 2 * 24 = 48.
9.
Soln:
The numbers formed must be of 4 digits. The digit in the thousand’s place must always be 4. For this, there is only one choice. After that, n = 6 – 1 = 5, r = 4 – 1 = 3. Then remaining 5 figures can be placed in remaining 3 places in:

Or, P(5,3) ways = $frac{{5!}}{{left( {5 - 3} right)!}}$ = $frac{{5!}}{{2!}}$ = $frac{{5{rm{*}}4{rm{*}}3{rm{*}}2{rm{*}}1}}{{2{rm{*}}1}}$ = 60 ways.
So, Total no.of ways by which 4 digits numbers between 4,000 and 5,000 can be formed = 1 * 60 = 60.

10.
Old Unit 2 Agendamrs. Colville's Math Classroom
Soln:
For the three digits numbers, there are 5 ways to fill in the 1st place, there are 4 ways to fill in the 2nd place and there are 3 ways to fill in the 3rd place. By the basic principle of counting, number of three digits numbers = 5 * 4 * 3 = 60.
Old Unit 2 Agendamrs. Colville's Math Classes
Again, for three digit numbers which are divisible by 5, the number in the unit place must be 5. So, the unit place can be filled up in 1 way. After filling up the unit place 4 numbers are left. Ten’s place can be filled up in 4 ways and hundredths place can be filled up in 3 ways. Then by the basic principle of counting, no.of 3 digits numbers which are divisible by 5 = 1 * 4 * 3 = 12.
